ART

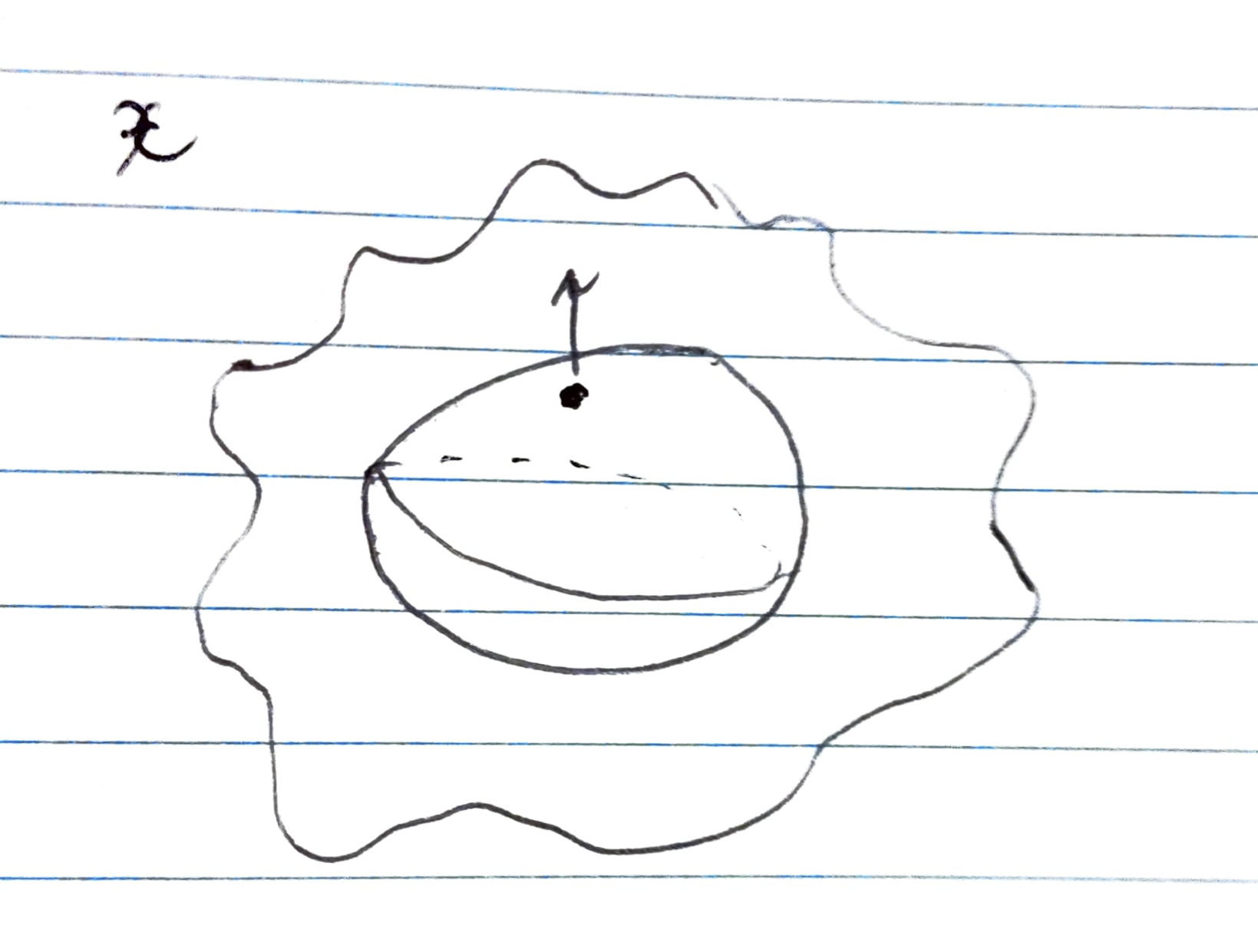
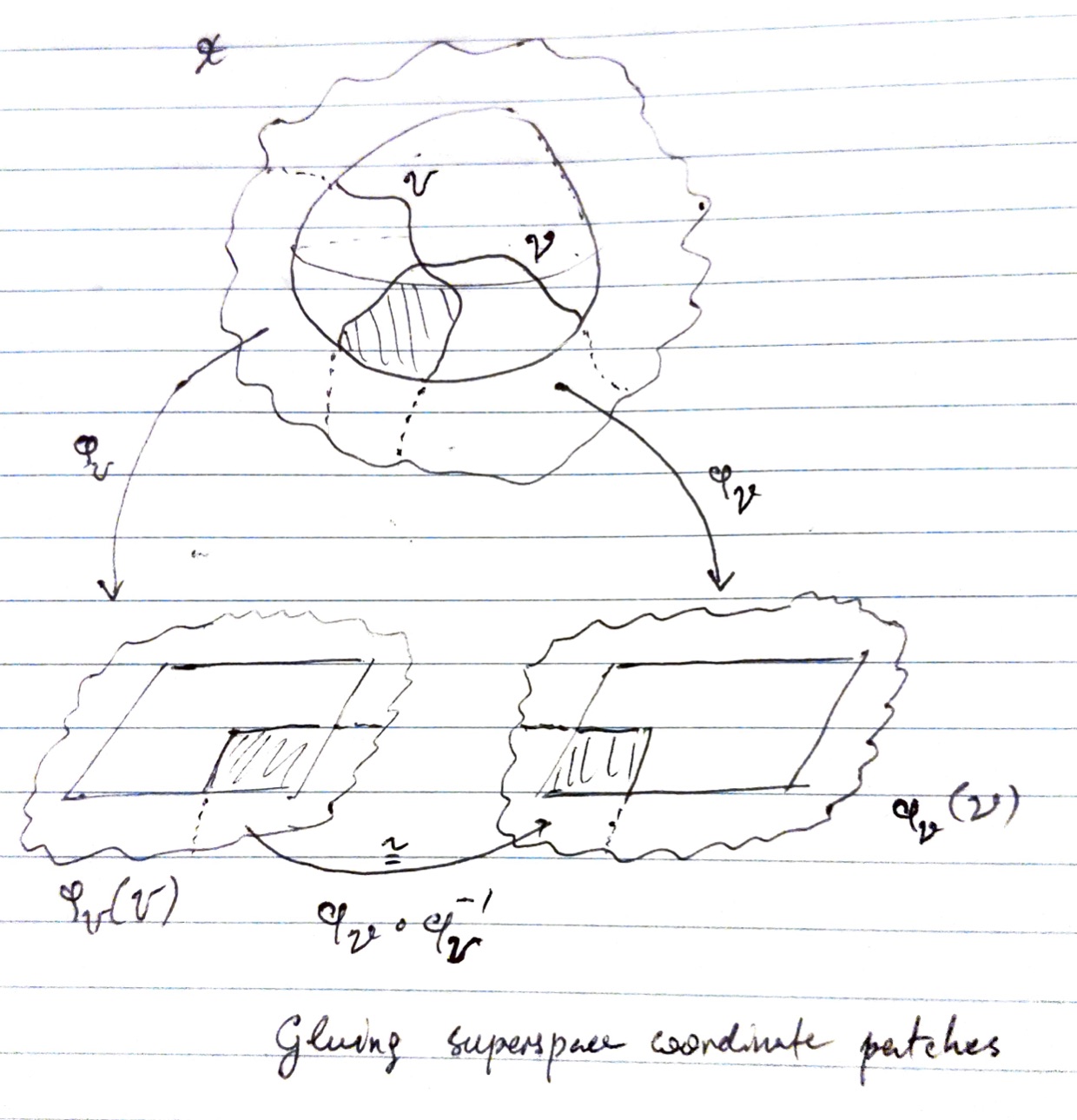
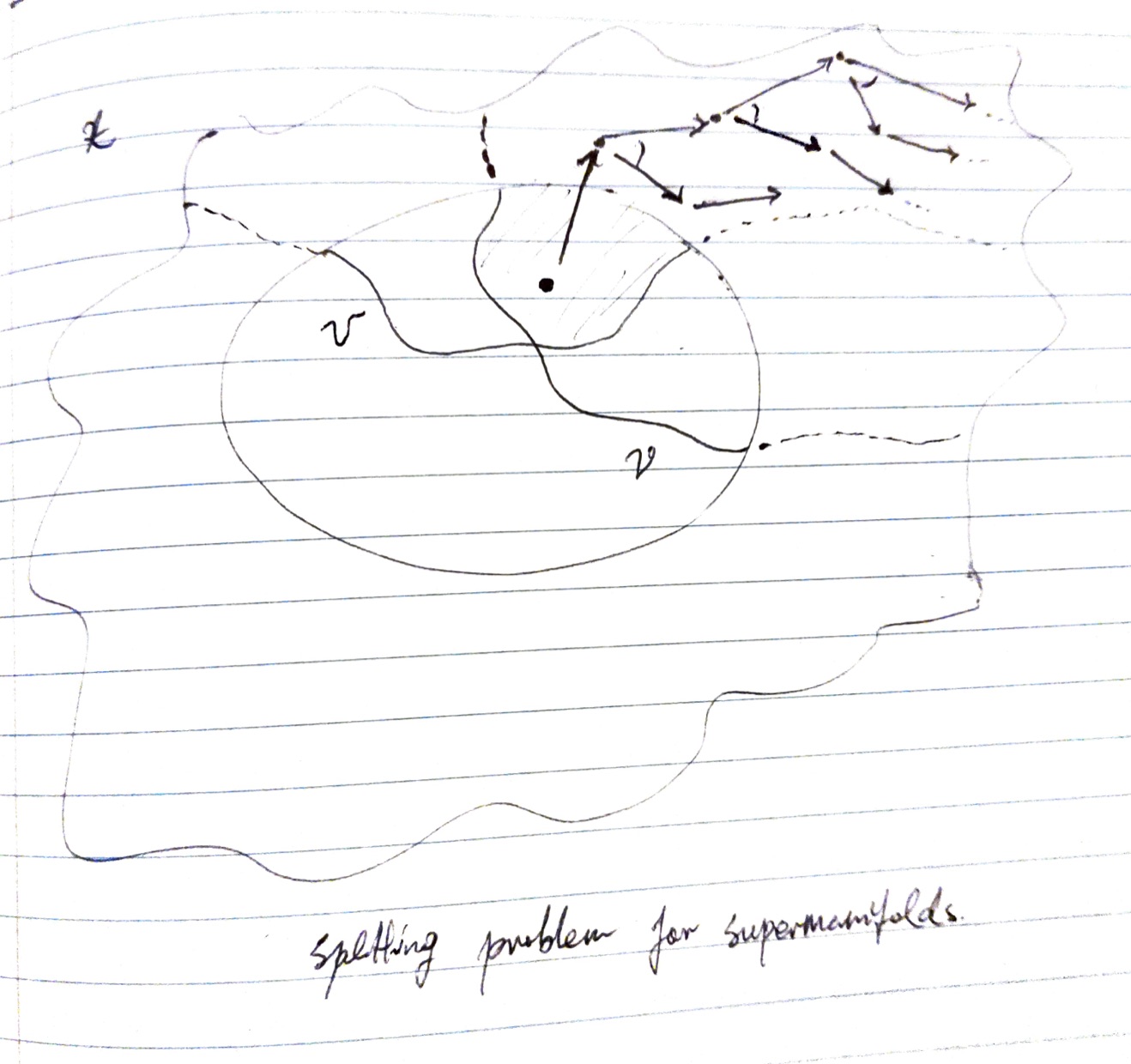
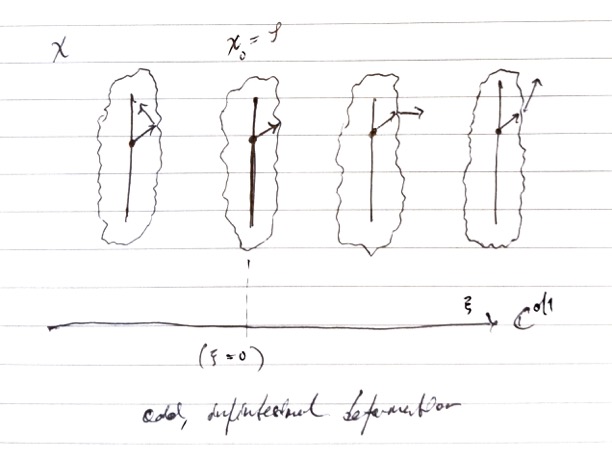
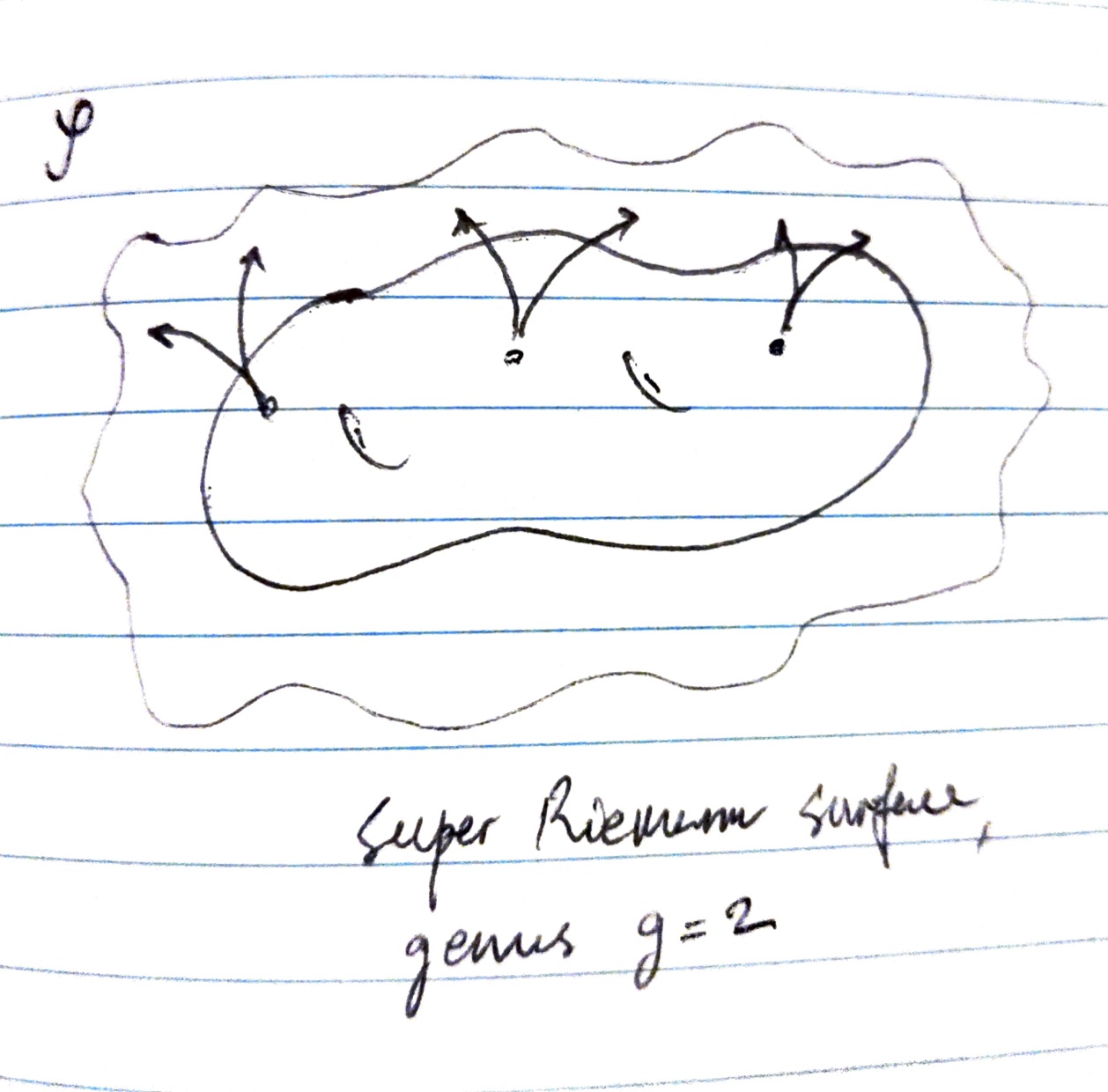
In this sketch we see what I imagine a supermanifold to be. Supermanifolds are mostly cloud-like objects with a material core, called its body. We can only see a supermanifold's body which, for mathematical purposes, is a classical space. Everything else outside the body and in the cloud-like strata is its soul. The soul cannot be observed directly. It can only be observed through its influence on the body.

Back to the specifics of the sketch, we see a sphere surrounded by a mysterious, wavy aura. The sphere is a classical space studied since antiquity. Its geometry was known at least as early as the Aristotlelian era to be non-Euclidean. The aura is a somewhat newer phenomenon. Mathematically, it represents the domain of totally anti-symmetric functions. Due to antisymmetry, all such functions vanish when taken to a suitably high, but finite, power. Hence in contrast with classic, Euclidean spaces, the aura itself cannot spread off to infinity. We can conclude, while we cannot see a supermanifold's soul, that it will nevertheless be constrained by its body.

Lastly, in the sketch it is emphasised that a point on a supermanifold comprises two parts: a point on the body and vector part extending outward into the soul. This vector part has infinitesimal length, much like the Newton-Leibnitz differential, \(dx\). We can get the general sense of where the vector is going but cannot see how far, as though driving through dense fog.

We learn in Calculus that to understand something is to understand how it can change infinitesimally in substance and form. The category-theorist might interject, we can only categorically understand something. This means, to understand something is to understand its relation to everything else in a category, whence inviting the interjection of the higher category-theorist: why stop at relations?

In this sketch we look to continue our journey to better understand supermanifolds. What we see here is a supermanifold spread out over an infinitesimal region. It is as though we sketched a figure on paper with a pencil and attempted to erase our drawing, leaving a smudge. Parameters defining the smudge will depend on the initial sketch. In mathematics-parlance, what we have drawn is an infinitesimal deformation.

In the center of our sketch is the original pencil drawing of our supermanifold, which is of a type we understand well. It is a split supermanifold. The property of "being split" is depicted by a straight line (body) surrounded by wavy aura (soul). The map \(\pi\) is a fibration allowing us to realise our deformation, \(\mathcal X\), as lying over the parameter space \(\mathbb A^{0|1}_{\mathbb C}\). As we vary the parameter \(\xi\) on \(\mathbb A_{\mathbb C}^{0|1}\) we vary the supermanifold lying over \(\xi\). Moving rightward or leftward results in a curving body representing more complicated, "non-split" supermanifolds. The totality of these images is our infinitesimal deformation.

A smooth function can be differentiated infinitely many times. Something similar could be said about a smooth space. If it is smooth we can start with its infinitesimal deformation, we can deform that; deform it again and so on ad infinitum.

In this sketch we see what a twice deformed, split supermanifold might look like. Recall, the infinitesimal deformation is a deformation over \(\mathbb A_{\mathbb C}^{0|1}\), i.e., over one dimension. In the sketch we see supermanifolds dancing, as it were, on a two-dimensional plane \(\mathbb A^{0|2}_{\mathbb C}\). There are two parameters to vary here: \( (\xi_1, \xi_2) \). Each instance will yield a supermanifold lying above them.

Observe in the sketch the 45-degree line \(\xi_1 = \xi_2\) over which lie copies of the split supermanifold. In contrast, along the \(\xi_1\) and \(\xi_2\)-axes are non-split supermanifolds, represented by curved bodies. This reflects how, in our sketch, a deformation can contain both split and non-split supermanifolds.

In my article, On the problem of splitting deformations of super Riemann surfaces, I study the deformation theory of a particular class of supermanifolds, called super Riemann surfaces. I present a conjectural characterization of deformations to all orders, which I checked to first (infinitesimal) and second order. Go read it and solve it!

Surgery is a major technique in geometric analysis. It was developed during the twentieth century and played an integral role in the solution of the famous Poincare conjecture.

In this sketch we see one manifestation of surgery, known in algebraic geometry as clutching. Starting with two spaces above, a torus with cusp and a 2-holed torus with cusp, the surgery \(f\) allows for glueing these cusps together and smoothing out the glued region. Cusps represent singular points, points at which "smoothness of structure" breaks down. What we gain in smoothness, by smoothing the cusp, we lose in complexity: we now have to work with three-holed tori.

A propagator in physics allows for calculating properties of information travelling along a communication channel. In this case, a particle at \(P\) communicating with a particle \(Q\). As depicted in the sketch on top, the particles \(P\) and \(Q\) are on distinct spaces, linked at a singular point barring communication. After surgery, see that communication is now possible albeit in the larger context of three-holed tori.

At the bottom of this sketch we see what we have referred to as the surgery \(f\) as an honest mathematical relation between mathematical objects. Surgery here is, mathematically, not a mapping between specific spaces such as the tori above; rather, it is a mapping between the parameter spaces of these tori.

Quantum mechanics distinguishes two types of fundamental particle: the boson and fermion. The physicists' tortoise and hare. The key distinguishing feature relates to the number operator. In a state \(|\Psi\rangle\) in a physical system, how many bosons and fermions can there be? The number operator will return any for bosons; one for fermions. Hence, any two bosons are identical from the quantum mechanics perspective. They can occupy the same state. Fermions in contrast are uniquely identifiable, one one per quantum state.

In this sketch we see an illustration of particle exchange, where the plane represents a particle state. Any number of bosons can occupy the same quantum state and so, supposing they were confined to a circle, we can exchange any two bosons \(b, b^\prime\) on the circle, leaving the state unchanged. On the right we exchange two fermions \(f, f^\prime\) but alas they cannot coexist in the same state. Exchanging the fermions require changing our quantum state, from the top plane to the bottom.

Blink and you might miss the fast moving hare; but not so for the glacially moving tortoise. Which particle type is most like the hare and which the tortoise?

This is our second sketch of an infinitesimal deformation. It is a more fine-grained look than our previous sketch. Here, we look to see what happens on the supermanifold itself as we vary the deformation parameter \(\xi\). Observe firstly that the body of our supermanifolds over each instance \(\xi\) is identical. What changes as we change our parameter are the points.

A point on a supermanifold is represented by a point on the body and a vector extending outwards, into the soul. The central fiber is the supermanifold over \(\xi=0\), which we see from the sketch is split. The property of "being split" amounts to understanding points as determined by their "classical part" and their "infinitesimal part". This is exactly what we see in the central fiber, being the supermanifold over \(\xi=0\). In nearby fibers however, taking them to be "non-split", points can no longer be understood by ther classical and infinitesimal parts alone.

In the sketch, points on nearby fibers are distinguished even though the classical and infinitesimal parts all coincide.

Imagine the Earth as depicted by pages of an atlas. The Earth and the atlas' pages are all instances of two dimensional spaces. Curiously enough, it is impossible to depict the Earth in its entirety by a one-page atlas. What this reveals is: the geometry of the Earth and that of a page are fundmantally different, even though they share the same dimension and can represent one another.

This subtlety underlies the flat Earth movement. That an atlas page represents part of the Earth demonstrates the Earth is locally flat. That a single atlas page cannot represent the entire Earth demonstrates the Earth is not globally flat.

In this sketch we see how superamanifolds can be understood in much the same way. Above we see represented a supermanifold in its entirety. Below we see pages of an atlas. The mappings \( \varphi_{\mathcal U}, \varphi_{\mathcal V} \) allow for establishing the correspondence between the local and global properties.

We have attempted in this sketch to depict the cornerstone problem in algebraic supergeometry: the splitting problem. On the split supermanifold, points are determined by their classical and infinitesimal part. The classical part lies on the body while the infinitesimal part extends out into the soul.

Observe in the sketch that the classical and infinitesimal parts of the point are fixed. Room for change is found in the extension of the point from its infinitesimal part through the higher stratospheres of the supermanifold.

We see in the sketch an angle parameter at each branching vertex where a different extension is possible. Mathematically, these angles form representatives of the cohomology group which parametrise all possible extensions; hence, all points.

While unproven as yet the idea behind this depiction is, if the supermanifold is split, an automorphism will send points to points in a way that preserves these angles, i.e., will be conformal.

We see in this sketch a genus two, super Riemann surface. Its body, being a classical space, is a genus two Riemann surface, or, a two-holed torus. As it is supermanifold, we see its soul represented by a wavy aura around the body.

Super Riemann surfaces were originally conceived by the string theorists' requirement for manifest supersymmetry in their physical theories. They have since flourished as an object of mathematical interest in the own right.

The soul cannot be depicted as straightforwardly as the body. The sketch however does provide a clue as to some further structure in the soul. Extending outward from the infinitesimal part, notice the bifurcation. To specify a super Riemann surface then it is necessary to choose a bifurcation, or, square root at each classical point. With this understood, we have taken a first step in our journey to better understand super Riemann surfaces.